Título: Tipos de integrales en cálculo: una guía completa
Introducción:
Bienvenidos al sitio "TiposDe", donde encontrarás información detallada y completa sobre diversos temas. En esta ocasión, nos adentraremos en el apasionante mundo de las integrales en cálculo. Las integrales son una herramienta fundamental en matemáticas, utilizadas para calcular áreas bajo una curva, encontrar volúmenes y resolver una amplia variedad de problemas.
En este artículo, exploraremos los diferentes tipos de integrales en cálculo, sus características y aplicaciones. Desde las integrales definidas e indefinidas hasta las integrales impropias, te brindaremos una visión general de cada uno para que puedas comprender su importancia y cómo utilizarlas en diversas situaciones.
Antes de sumergirnos en los tipos de integrales, es importante recordar que el cálculo integral es una rama de las matemáticas desarrollada por Isaac Newton y Gottfried Leibniz en el siglo XVII. Desde entonces, ha sido una herramienta fundamental en diversas áreas como la física, la ingeniería y la economía, permitiendo resolver problemas de optimización, modelado y más.
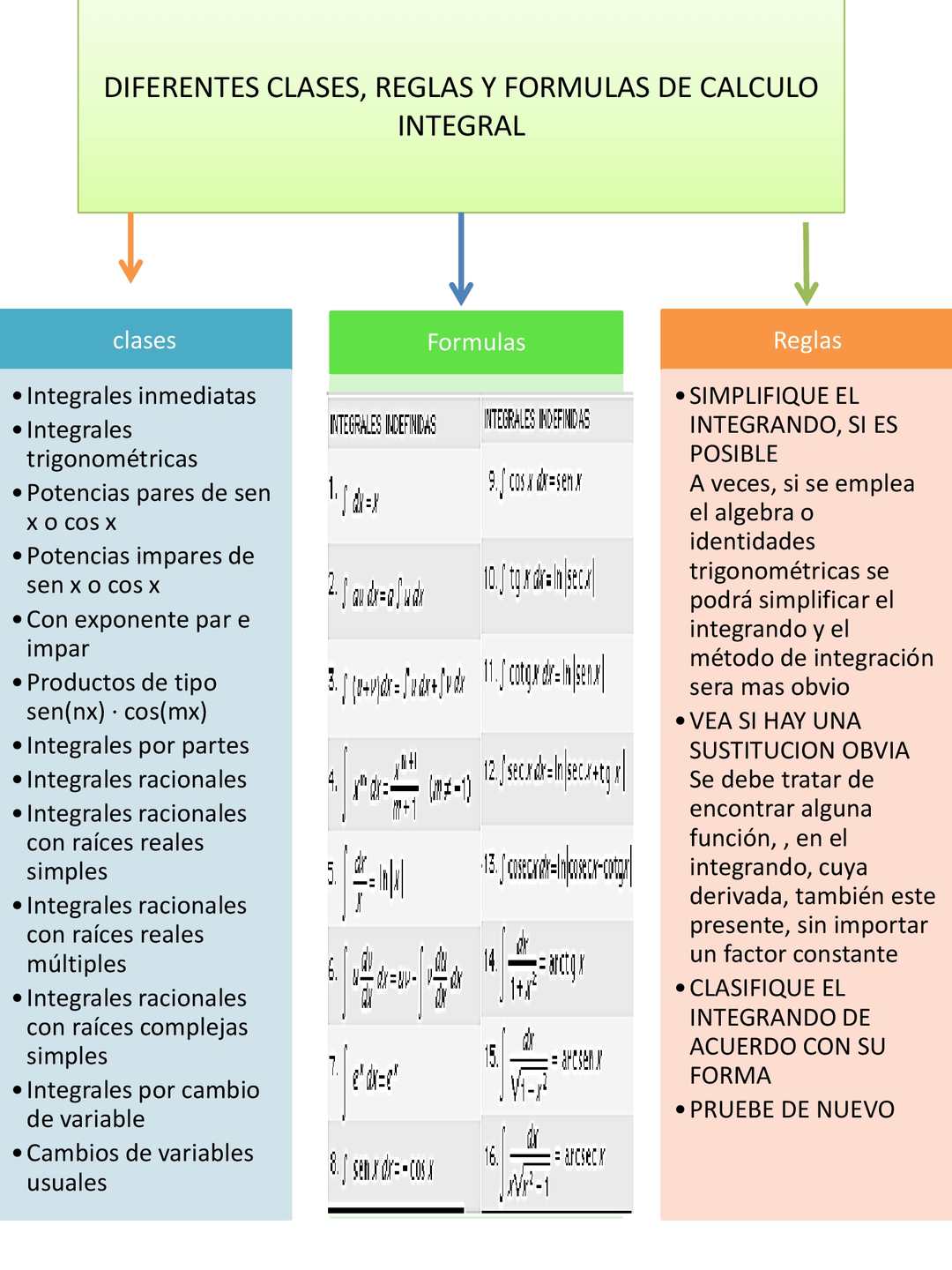
Tipos de Integrales IndefinidasTítulo: Tipos de integrales en cálculo
-
Integrales definidas
Las integrales definidas son aquellas en las que se conoce el intervalo de integración. Representan el área exacta bajo una curva dentro de un límite determinado. La notación utilizada es la siguiente: ∫(a,b) f(x) dx, donde "a" y "b" representan los límites inferior y superior del intervalo, respectivamente. Estas integrales son útiles para calcular áreas, volúmenes y valores promedio, entre otras aplicaciones.
-
Integrales indefinidas
Las integrales indefinidas son aquellas en las que no se especifica el intervalo de integración. Representan una familia de funciones primitivas o antiderivadas de una función dada. La notación utilizada es la siguiente: ∫f(x) dx. Al realizar una integral indefinida, obtenemos una función más general, en lugar de un valor numérico. Estas integrales son fundamentales para el cálculo diferencial y la obtención de funciones primitivas.
-
Integrales impropias
Las integrales impropias son aquellas en las que al menos uno de los límites de integración es infinito o la función posee una discontinuidad en el intervalo de integración. Estas integrales representan conceptos límite y se utilizan para calcular áreas o valores en situaciones donde las integrales definidas no son aplicables directamente. Para evaluar estas integrales, es necesario utilizar técnicas especiales como las series de Taylor o los límites.
-
Integrales múltiples
Las integrales múltiples son aquellas en las que se integra una función de varias variables sobre una región en el espacio. Estas integrales se utilizan para calcular volúmenes, áreas y otros conceptos similares en espacios tridimensionales o de mayor dimensión. La notación utilizada depende del número de variables y el tipo de región sobre la cual se integra.
Tipos de intervalos desigualdades -
Integrales de línea
Las integrales de línea son aquellas en las que se integra una función vectorial a lo largo de una curva en el espacio. Estas integrales se utilizan en el campo de la física y la ingeniería para calcular trabajo, circulación de campos vectoriales y otras cantidades relacionadas con trayectorias curvilíneas.
-
Integrales de superficie
Las integrales de superficie son aquellas en las que se integra una función vectorial sobre una superficie en el espacio. Estas integrales son utilizadas en física para calcular el flujo de campos vectoriales a través de superficies cerradas o abiertas. También se aplican en áreas como la geometría diferencial y el análisis numérico.
-
Integrales de volumen
Las integrales de volumen son aquellas en las que se integra una función escalar o vectorial para calcular el volumen de un sólido en el espacio. Estas integrales se utilizan en diversas áreas como la física, la ingeniería y la geometría para determinar volúmenes de objetos tridimensionales y resolver problemas de naturaleza geométrica.
-
Integrales de Fourier
Las integrales de Fourier son aquellas que permiten descomponer una función periódica en una suma de funciones senoidales. Estas integrales se utilizan ampliamente en análisis de señales, procesamiento de imágenes y otras áreas de la física y la ingeniería. La teoría de Fourier es fundamental para comprender el comportamiento de las ondas y la transformada de Fourier es una herramienta clave en el análisis de señales.
-
Integrales de Laplace
Las integrales de Laplace son aquellas que permiten transformar una ecuación diferencial en el dominio del tiempo a una ecuación algebraica en el dominio de la frecuencia. Estas integrales se utilizan en el estudio de sistemas lineales y su respuesta a diferentes señales de entrada. La transformada de Laplace es una herramienta esencial en el análisis de circuitos eléctricos y sistemas de control.
Tipos de intervalos en inecuaciones -
Integrales de aires y áreas
Estas integrales se utilizan para calcular áreas en situaciones donde las integrales definidas no son aplicables directamente, como áreas entre curvas o áreas de figuras no regulares. También se utilizan en análisis estadístico y en cálculo de probabilidades para determinar áreas bajo curvas de densidad de probabilidad. Aunque su aplicación es más específica, su comprensión es fundamental para un conocimiento completo del cálculo integral.
Sección de preguntas frecuentes:
-
¿Cuál es la diferencia entre una integral definida e indefinida?
La diferencia radica en que en la integral definida se conoce el intervalo de integración, mientras que en la integral indefinida no se especifica dicho intervalo. Además, la integral definida representa un valor numérico, mientras que la integral indefinida representa una función.
-
¿En qué situaciones se utilizan las integrales impropias?
Las integrales impropias se utilizan en situaciones donde los límites de integración son infinitos o la función presenta una discontinuidad en el intervalo. Estas integrales representan casos límite y se utilizan para calcular áreas o valores en estas situaciones especiales.
-
¿Qué aplicaciones tienen las integrales múltiples en la vida cotidiana?
Las integrales múltiples tienen aplicaciones en campos como la física, la ingeniería y la economía. Se utilizan para calcular volúmenes, áreas y otros conceptos en espacios tridimensionales o de mayor dimensión. Por ejemplo, en física, se pueden utilizar para calcular la masa o el centro de masa de objetos irregulares.
Tipos de intervalos matemáticas -
¿Cuál es la importancia de las integrales en el campo de la ingeniería?
Las integrales son fundamentales en ingeniería, ya que permiten resolver problemas de optimización, modelado y análisis de sistemas. Por ejemplo, en ingeniería civil, las integrales se utilizan para calcular la resistencia de materiales y determinar las deformaciones en estructuras. En ingeniería eléctrica, se utilizan para analizar circuitos y diseñar sistemas de control.
-
¿Qué es la transformada de Fourier y en qué se aplica?
La transformada de Fourier es una herramienta matemática que permite descomponer una función periódica en una suma de funciones senoidales. Se utiliza en análisis de señales, procesamiento de imágenes, reconocimiento de patrones y otras áreas de la física y la ingeniería. Permite analizar el contenido frecuencial de una señal y es esencial en el campo de las telecomunicaciones.
Conclusión:
En conclusión, conocer los diferentes tipos de integrales en cálculo es fundamental para comprender su importancia y aplicaciones en diversas áreas. Desde las integrales definidas e indefinidas hasta las integrales impropias, múltiples, de línea y de superficie, cada tipo tiene sus propias características y se utiliza en situaciones específicas.
Las integrales son una herramienta poderosa y versátil para resolver problemas matemáticos y físicos. Desde calcular áreas y volúmenes hasta analizar señales y diseñar sistemas, su aplicación es amplia y diversa. El dominio del cálculo integral es esencial para estudiantes de ciencia, tecnología, ingeniería y matemáticas, así como para profesionales en campos relacionados.
Tipos de límites en cálculo diferencialAgradecemos tu tiempo y esperamos que esta guía sobre los tipos de integrales en cálculo te haya resultado útil y enriquecedora. Si tienes comentarios, dudas o sugerencias, no dudes en dejarlas en la sección de comentarios. Nos encantaría conocer tu opinión y seguir brindándote contenido de calidad en "tiposde.net". ¡Hasta la próxima!
Si quieres conocer otros artículos parecidos a Tipos de integrales en cálculo puedes visitar la categoría Matemáticas.

Conoce mas Tipos