Tipos de funciones cuadráticas

Las funciones cuadráticas son una herramienta fundamental en el estudio del álgebra, especialmente en el cálculo del movimiento y la resolución de ecuaciones. En este artículo vamos a explorar los diferentes tipos de funciones cuadráticas y cómo se utilizan en la práctica.

En primer lugar, es importante recordar que las funciones cuadráticas son aquellas que tienen la forma de ax^2 + bx + c, donde a, b y c son constantes. Estas funciones son únicas porque tienen una curva en forma de U, también conocida como parábola. La posición y la dirección de la parábola dependen de los valores de a, b y c.

En este artículo, vamos a ver los diferentes tipos de funciones cuadráticas y cuáles son sus características principales. Si estás interesado en aprender más sobre este tema, estás en el lugar correcto.

Tipos de funciones cuadráticas

1. Función cuadrática estándar

   La función cuadrática estándar es la forma más básica de la función cuadrática. Tiene la forma de y = ax^2 + bx + c, donde a, b y c son constantes que definen la posición y la forma de la parábola.

2. Función cuadrática en vértice

   La función cuadrática en vértice es una variación de la función cuadrática estándar. Esta función se utiliza para encontrar la posición del vértice de la parábola. Para la función cuadrática en vértice, la ecuación tiene la forma de y = a(x-h)^2 + k, donde (h, k) es el vértice de la parábola.

   Tipos de funciones de varias variables

3. Función cuadrática factorizada

   La función cuadrática factorizada se utiliza para encontrar las raíces de la parábola. Esta función tiene la forma de y = a(x-x1)(x-x2), donde x1 y x2 son las raíces de la parábola.

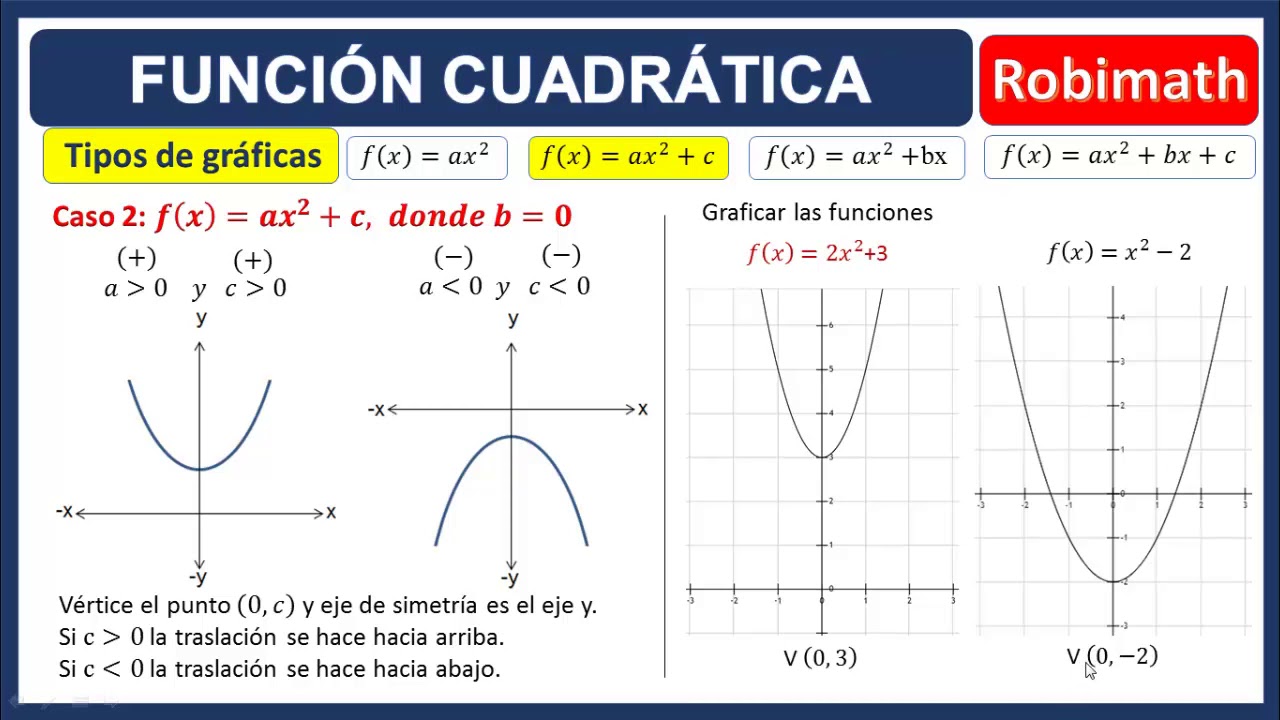
4. Función cuadrática de la forma ax^2 + c

   La función cuadrática de la forma ax^2 + c es una variación de la función cuadrática estándar. En esta función, la constante b se omite, lo que significa que la parábola no se mueve horizontalmente. Esta función se utiliza comúnmente para modelar el movimiento vertical.

5. Función cuadrática de la forma a(x-h)^2 + c

   La función cuadrática de la forma a(x-h)^2 + c es similar a la función cuadrática estándar en vértice. Sin embargo, en este caso, la parábola no se mueve verticalmente. Esta función se utiliza comúnmente para modelar el movimiento horizontal.

6. Función cuadrática simétrica

   La función cuadrática simétrica es una función en la que el vértice de la parábola está en el origen de coordenadas. Es decir, la ecuación de esta función tiene la forma y = ax^2 o y = -ax^2.

7. Función cuadrática par

   La función cuadrática par es una función simétrica respecto al eje y. Es decir, la ecuación de esta función tiene la forma y = ax^2 o y = -ax^2.

   Tipos de funciones especiales matemáticas

8. Función cuadrática impar

   La función cuadrática impar es una función antisimétrica respecto al eje y. Es decir, la ecuación de esta función tiene la forma y = ax^3 o y = -ax^3.

9. Función cuadrática con vértice en (h, k)

   La función cuadrática con vértice en (h, k) tiene una ecuación de la forma y = a(x-h)^2 + k. Esta ecuación se utiliza comúnmente para modelar la posición de la parábola.

10. Función cuadrática con vértice en (0, 0)

    La función cuadrática con vértice en (0, 0) es una forma especial de la función cuadrática que tiene la forma y = ax^2. Esta ecuación se utiliza comúnmente para modelar la velocidad o la aceleración en el movimiento.

11. Función cuadrática con raíces reales distintas

    La función cuadrática con raíces reales distintas tiene una ecuación de la forma y = a(x-x1)(x-x2), donde x1 y x2 son dos números reales distintos. Esta función se utiliza comúnmente para modelar la cantidad de tiempo que tarda una partícula en caer en la tierra desde una cierta altura.

12. Función cuadrática con raíces reales iguales

    La función cuadrática con raíces reales iguales se utiliza cuando los dos números reales son iguales. Esta función se utiliza comúnmente para encontrar el área de un cuadrado.

    Tipos de funciones exponenciales

13. Función cuadrática con raíces imaginarias

    La función cuadrática con raíces imaginarias no tiene soluciones reales. Esta función se utiliza comúnmente para modelar el movimiento de un objeto en una dimensión compleja.

14. Función cuadrática con un eje de simetría vertical

    La función cuadrática con un eje de simetría vertical tiene una forma de y = a(x-h)^2 + k, donde h es la coordenada horizontal del eje de simetría. Esta función se utiliza comúnmente para modelar la posición y el movimiento de un objeto que se desplaza en una dimensión.

15. Función cuadrática con un eje de simetría horizontal

    La función cuadrática con un eje de simetría horizontal tiene una forma de y = a(x-h)^2 + k, donde k es la coordenada vertical del eje de simetría. Esta función se utiliza comúnmente en la arquitectura y la ingeniería para diseñar y construir estructuras que son estables y eficientes.

16. Función cuadrática en pendiente - intercepto

    La función cuadrática en pendiente - intercepto tiene una forma de y = ax^2 + bx + c. Esta función se utiliza comúnmente para encontrar la intersección de dos líneas en un plano bidimensional.

17. Función cuadrática en forma de cerradura o pestillo

    La función cuadrática en forma de cerradura o pestillo tiene una forma de y = ax^2 + bx + c, donde a es negativo. Esta función se utiliza comúnmente para modelar el movimiento de una puerta o una cerradura.

    Tipos de funciones inversas

18. Función cuadrática con una transformación lineal

    La función cuadrática con una transformación lineal es una función de la forma y = a(f(x - h)) + k, donde f(x) es una función lineal. Esta función se utiliza comúnmente en el procesamiento de señales y en el diseño de sistemas de control.

19. Función cuadrática con una transformación exponencial

    La función cuadrática con una transformación exponencial es una función de la forma y = a(e^bx + c). Esta función se utiliza comúnmente en la química y la biología para modelar el crecimiento exponencial de una población o la descomposición de una sustancia química.

Preguntas frecuentes

1. ¿Cómo se puede utilizar una función cuadrática?

   Las funciones cuadráticas se utilizan para modelar una variedad de fenómenos físicos y matemáticos, desde el movimiento y la aceleración hasta la resolución de ecuaciones y la optimización de sistemas.

2. ¿Cuál es la fórmula para encontrar el vértice de una función cuadrática?

   La fórmula para encontrar el vértice de una función cuadrática en vértice es (h, k), donde h = -b/(2a) y k = f(h).

3. ¿Cómo se puede encontrar las raíces de una función cuadrática?

   Las raíces de una función cuadrática se pueden encontrar utilizando la fórmula general de la ecuación cuadrática, que es x = [-b ± sqrt(b^2 - 4ac)]/2a.

   Tipos de funciones lineales

4. ¿Cómo se puede simplificar una función cuadrática?

   Una función cuadrática se puede simplificar utilizando factores comunes y la factorización de expresiones cuadráticas.

5. ¿Cuál es la fórmula para la altura máxima de una parábola?

   La fórmula para encontrar la altura máxima de una parábola es k = c - (b^2/(4a)).

Conclusión

En conclusión, las funciones cuadráticas son una herramienta fundamental en el estudio del álgebra y la matemática. En este artículo, hemos explorado los diferentes tipos de funciones cuadráticas que existen y cómo se utilizan en la práctica.

Esperamos haber sido capaces de proporcionar una comprensión clara y concisa de estas funciones y cómo se aplican en diversos campos. Si tienes alguna pregunta o comentario sobre este tema, no dudes en dejarnos un mensaje en la sección de comentarios.

Gracias por leer!

Tenemos muchos mas temas relacionados con Tipos de funciones cuadráticas te invitamos a que visites el tema de Matemáticas y te pongas al día con conocimientos sorprendentes!.