Tipos de funciones trigonométricas

Las funciones trigonométricas son muy importantes en la matemática y en muchas otras áreas de estudio. La trigonometría se estudia desde el colegio, y sus aplicaciones se pueden encontrar en casi cualquier disciplina científica y técnica de la actualidad.

En este artículo vamos a repasar los diferentes tipos de funciones trigonométricas que se utilizan para describir diferentes aspectos de las relaciones entre los ángulos y los lados de los triángulos. Esperamos que esta guía te resulte útil y te ayude a entender mejor la trigonometría y sus aplicaciones.

Es importante recordar que la notación de las funciones trigonométricas puede variar según el país y la escuela, así que no te sorprendas si encuentras algunas diferencias entre la notación que utilizamos aquí y la que se utiliza en tu propio país o institución académica. En cualquier caso, las definiciones de las funciones son las mismas, así que no te preocupes demasiado por esto.

Tipos de funciones trigonométricas

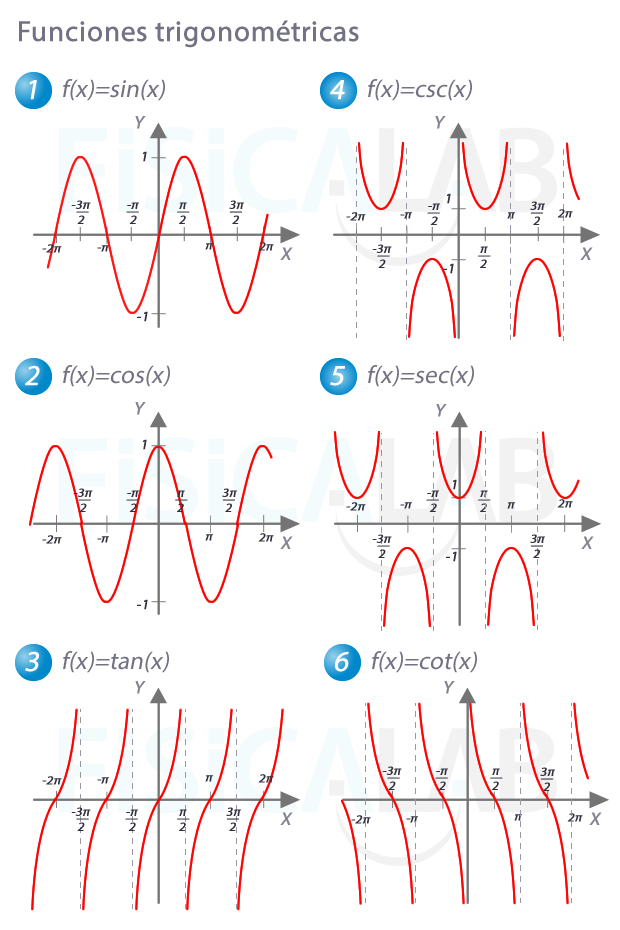
1. Función seno

   La función seno se define como la relación entre el lado opuesto a un ángulo y la hipotenusa de un triángulo rectángulo. Esta función se denota como sin(x), donde x es el ángulo en radianes.

2. Función coseno

   La función coseno se define como la relación entre el lado adyacente a un ángulo y la hipotenusa de un triángulo rectángulo. Esta función se denota como cos(x), donde x es el ángulo en radianes.

   Tipos de geometría

3. Función tangente

   La función tangente se define como la relación entre el lado opuesto a un ángulo y el lado adyacente a ese mismo ángulo en un triángulo rectángulo. Esta función se denota como tan(x), donde x es el ángulo en radianes.

4. Función cotangente

   La función cotangente se define como la relación entre el lado adyacente a un ángulo y el lado opuesto a ese mismo ángulo en un triángulo rectángulo. Esta función se denota como cot(x), donde x es el ángulo en radianes.

5. Función secante

   La función secante se define como el inverso de la función coseno. Es decir, la relación entre la hipotenusa y el lado adyacente a un ángulo en un triángulo rectángulo. Esta función se denota como sec(x), donde x es el ángulo en radianes.

6. Función cosecante

   La función cosecante se define como el inverso de la función seno. Es decir, la relación entre la hipotenusa y el lado opuesto a un ángulo en un triángulo rectángulo. Esta función se denota como csc(x), donde x es el ángulo en radianes.

7. Función arcoseno

   La función arcoseno es la inversa de la función seno. Es decir, si y = sin(x), entonces x = arcsin(y). Esta función devuelve el ángulo cuyo seno es igual a y. Esta función se denota como arcsin(x), donde x es un número entre -1 y 1.

   Tipos de gráficas matemáticas

8. Función arcocoseno

   La función arcocoseno es la inversa de la función coseno. Es decir, si y = cos(x), entonces x = arccos(y). Esta función devuelve el ángulo cuyo coseno es igual a y. Esta función se denota como arccos(x), donde x es un número entre -1 y 1.

9. Función arcotangente

   La función arcotangente es la inversa de la función tangente. Es decir, si y = tan(x), entonces x = arctan(y). Esta función devuelve el ángulo cuya tangente es igual a y. Esta función se denota como arctan(x), donde x es cualquier número real.

10. Función arcoctangente

    La función arcoctangente es la inversa de la función cotangente. Es decir, si y = cot(x), entonces x = arccot(y). Esta función devuelve el ángulo cuya cotangente es igual a y. Esta función se denota como arccot(x), donde x es cualquier número real.

11. Función seno hiperbólico

    La función seno hiperbólico se define como la relación entre el lado opuesto a un ángulo hiperbólico y la hipotenusa en un triángulo hiperbólico. Esta función se denota como sinh(x), donde x es un número real.

12. Función coseno hiperbólico

    La función coseno hiperbólico se define como la relación entre el lado adyacente a un ángulo hiperbólico y la hipotenusa en un triángulo hiperbólico. Esta función se denota como cosh(x), donde x es un número real.

    Tipos de Hiperbola

13. Función tangente hiperbólica

    La función tangente hiperbólica se define como la relación entre el lado opuesto a un ángulo hiperbólico y el lado adyacente a ese mismo ángulo en un triángulo hiperbólico. Esta función se denota como tanh(x), donde x es un número real.

14. Función cotangente hiperbólica

    La función cotangente hiperbólica se define como la relación entre el lado adyacente a un ángulo hiperbólico y el lado opuesto a ese mismo ángulo en un triángulo hiperbólico. Esta función se denota como coth(x), donde x es un número real.

15. Función secante hiperbólica

    La función secante hiperbólica se define como el inverso de la función coseno hiperbólico. Es decir, la relación entre la hipotenusa y el lado adyacente a un ángulo hiperbólico. Esta función se denota como sech(x), donde x es un número real.

16. Función cosecante hiperbólica

    La función cosecante hiperbólica se define como el inverso de la función seno hiperbólico. Es decir, la relación entre la hipotenusa y el lado opuesto a un ángulo hiperbólico. Esta función se denota como csch(x), donde x es un número real.

17. Función arcoseno hiperbólico

    La función arcoseno hiperbólico es la inversa de la función seno hiperbólico. Es decir, si y = sinh(x), entonces x = arcsinh(y). Esta función devuelve el ángulo hiperbólico cuyo seno hiperbólico es igual a y. Esta función se denota como arcsinh(x), donde x es cualquier número real.

    Tipos de homotecia que existen

18. Función arcocoseno hiperbólico

    La función arcocoseno hiperbólico es la inversa de la función coseno hiperbólico. Es decir, si y = cosh(x), entonces x = arccosh(y). Esta función devuelve el ángulo hiperbólico cuyo coseno hiperbólico es igual a y. Esta función se denota como arccosh(x), donde x es un número mayor o igual a 1.

19. Función arcotangente hiperbólica

    La función arcotangente hiperbólica es la inversa de la función tangente hiperbólica. Es decir, si y = tanh(x), entonces x = arctanh(y). Esta función devuelve el ángulo hiperbólico cuya tangente hiperbólica es igual a y. Esta función se denota como arctanh(x), donde x es un número real entre -1 y 1.

20. Función arcoctangente hiperbólica

    La función arcoctangente hiperbólica es la inversa de la función cotangente hiperbólica. Es decir, si y = coth(x), entonces x = arccoth(y). Esta función devuelve el ángulo hiperbólico cuya cotangente hiperbólica es igual a y. Esta función se denota como arccoth(x), donde x es un número mayor que 1.

Preguntas frecuentes

1. ¿Cómo se calcula el seno de un ángulo?

   El seno de un ángulo se calcula dividiendo la longitud del lado opuesto al ángulo por la longitud de la hipotenusa en un triángulo rectángulo.

2. ¿Cómo se calcula la tangente de un ángulo?

   La tangente de un ángulo se calcula dividiendo la longitud del lado opuesto al ángulo por la longitud del lado adyacente a ese mismo ángulo en un triángulo rectángulo.

   Tipos de identidades trigonométricas

3. ¿Por qué se usan las funciones trigonométricas?

   Las funciones trigonométricas se utilizan para describir las relaciones entre los ángulos y los lados de los triángulos, y estas relaciones son muy útiles en muchas áreas de estudio, desde la geometría hasta la física, la ingeniería y muchas más.

4. ¿Para qué se utilizan las funciones trigonométricas hiperbólicas?

   Las funciones trigonométricas hiperbólicas son útiles en muchos cálculos matemáticos y físicos, especialmente en la teoría de funciones especiales y en la teoría de la relatividad.

5. ¿Es posible utilizar las funciones trigonométricas en la vida cotidiana?

   Aunque no lo parezca, las funciones trigonométricas se utilizan en muchas situaciones cotidianas, desde el diseño y la construcción de edificios y puentes hasta la navegación y la astronomía.

Conclusión

Las funciones trigonométricas son herramientas fundamentales en la matemática y en muchas otras áreas de estudio. Con ellas podemos describir las relaciones entre los ángulos y los lados de los triángulos, y utilizar esas relaciones para resolver muchos problemas interesantes y útiles.

Esperamos que esta guía te haya resultado útil para entender mejor los diferentes tipos de funciones trigonométricas que existen y sus aplicaciones en diversas disciplinas. Si tienes alguna pregunta o comentario, no dudes en dejarlos en la sección de comentarios a continuación, ¡estaremos encantados de responderte!

¡Gracias por leernos!

Si quieres conocer otros artículos parecidos a Tipos de funciones trigonométricas puedes visitar la categoría Matemáticas.