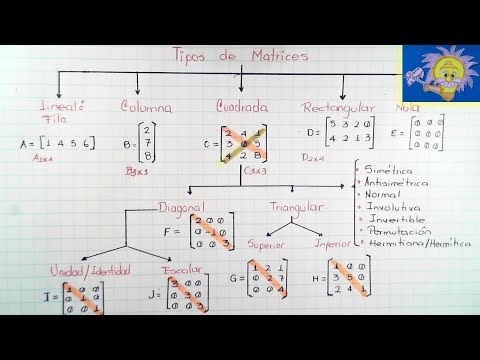
Tipos de matrices cuadradas
Introducción:
Las matrices cuadradas son una herramienta fundamental en el ámbito de las matemáticas. Son utilizadas en diversas áreas como el álgebra lineal, las ciencias de la computación y la estadística. En este artículo, exploraremos los diferentes tipos de matrices cuadradas y sus características principales. Si eres un estudiante de matemáticas o simplemente tienes curiosidad por aprender más sobre este tema, has llegado al lugar indicado.
Las matrices cuadradas se caracterizan por tener el mismo número de filas y columnas. Esto significa que su tamaño es siempre de nxn, donde n representa el número de filas o columnas. Estas matrices tienen muchas propiedades y aplicaciones, por lo que es crucial comprender los diferentes tipos que existen.
A continuación, enumeraremos los tipos más comunes de matrices cuadradas y describiremos sus características distintivas. ¡Vamos a empezar!
Tipos de matrices cuadradas:
-
Matriz identidad
La matriz identidad se caracteriza por tener unos en su diagonal principal y ceros en el resto de elementos. Se representa como I.
Tipos de Medición Estadística -
Matriz nula
La matriz nula es aquella en la que todos sus elementos son cero. Se representa como O.
-
Matriz diagonal
La matriz diagonal es aquella en la que todos los elementos fuera de la diagonal principal son cero.
-
Matriz triangular superior
La matriz triangular superior es aquella en la que todos los elementos por debajo de la diagonal principal son
ceros. -
Matriz triangular inferior
La matriz triangular inferior es aquella en la que todos los elementos por encima de la diagonal principal son
ceros. -
Matriz escalar
La matriz escalar es aquella en la que todos los elementos de la diagonal principal son iguales y los demás elementos son ceros.
Tipos de medidas -
Matriz simétrica
La matriz simétrica es aquella en la que la matriz es igual a su traspuesta.
-
Matriz antisimétrica
La matriz antisimétrica es aquella en la que la matriz traspuesta es igual a la matriz negativa.
-
Matriz ortogonal
La matriz ortogonal es aquella en la que la matriz es igual a su inversa. Además, sus columnas son vectores ortonormales.
-
Matriz invertible
La matriz invertible es aquella que tiene inversa. La matriz inversa de una matriz cuadrada A se representa como A^-1.
Preguntas frecuentes:
-
¿Cuáles son las aplicaciones de las matrices cuadradas?
Las matrices cuadradas tienen numerosas aplicaciones en áreas como la física, la informática, la economía y la
Tipos de métodos de factorización
ingeniería. Se utilizan para resolver sistemas de ecuaciones, calcular transformaciones lineales, representar
redes y modelar fenómenos en la física y la economía, entre otros. -
¿Cómo se calcula la inversa de una matriz cuadrada?
El cálculo de la inversa de una matriz cuadrada puede realizarse mediante diferentes métodos, como la eliminación
de Gauss-Jordan o la regla de Cramer. Estos métodos permiten encontrar la matriz inversa, siempre y cuando
exista. -
¿Qué es una matriz singular?
Una matriz cuadrada se considera singular si no tiene inversa. Esto ocurre cuando su determinante es cero.
-
¿Cómo se multiplican matrices cuadradas?
La multiplicación de matrices cuadradas se realiza combinando las filas de la primera matriz con las columnas
de la segunda matriz de acuerdo con las reglas del álgebra lineal. El resultado es una nueva matriz que
representa la combinación lineal de las matrices originales. -
¿Qué es la traspuesta de una matriz?
La traspuesta de una matriz se obtiene intercambiando las filas por columnas. Es decir, el elemento que estaba en
la posición (i, j) en la matriz original estará en la posición (j, i) en la matriz traspuesta.
Conclusión:
En resumen, las matrices cuadradas son una herramienta esencial en matemáticas y tienen diversas aplicaciones en varias
disciplinas. En este artículo, hemos discutido los tipos más comunes de matrices cuadradas, como la matriz identidad,
la matriz diagonal y la matriz simétrica, entre otras.
Espero que esta información te haya resultado útil y haya respondido a tus preguntas sobre los diferentes tipos de matrices
cuadradas. Si tienes alguna duda o comentario, no dudes en dejarlo en la sección de comentarios. ¡Agradezco tu participación
y espero saber tu opinión sobre este tema!
Gracias por leer y ¡hasta la próxima!
Si quieres conocer otros artículos parecidos a Tipos de matrices cuadradas puedes visitar la categoría Matemáticas.

Conoce mas Tipos